対数軸のスケーリングでは、MajorUnit が係数として各サイクルの底の値に掛けられて、対数の底の各サイクルにおける目盛りの間隔を決定します。つまり、(MajorUnit * 底サイクル値) は、各サイクル内の目盛りの増分とほぼ同じ値になります。対数の底が整数値の場合、結果は通常、そのままの値です。浮動小数点値の場合、目盛り値は線形スケーリングと同様に、適切な数値に丸められます。

UnitMajor と対数軸の詳細

多くの場合、対数スケールを使用すると、グラフ軸の範囲は対数の底の複数のサイクルにまたがります。その場合、あるサイクルに適した値も、その前後のサイクルにとってはほとんど意味がないので、MajorUnit を通常のように線形的に指定しても意味がありません。MajorUnit の設定を有効に利用するには、対数の底の各サイクルに対応した値にする必要があります。

これで適切に対応できない場合は、この軸に使用できる単一値、固定値、または増分値を検討します。

上記の理由により、対数軸のグラフでは、MajorUnit には各サイクルの底の値分の１が指定されていると見なされます。次の例を考えます。

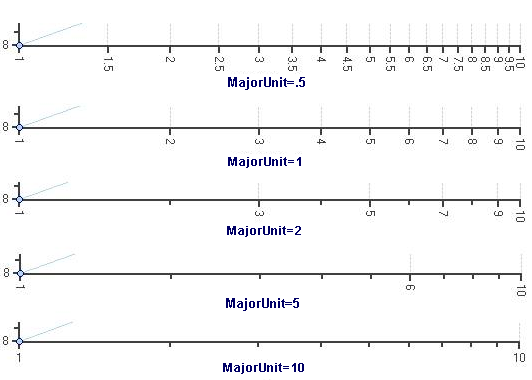
それぞれのケースの底サイクル値は１です。各サイクルにおいて、次の目盛り値 = 前の数値 + (サイクルの底の値 * MajorUnit) になります。MajorUnit の最大値は LogarithmicBase です。MajorUnit の自動設定値は、常に LogBase です。

すべての目盛り値が計算されると、数値を読みやすくするために一定の丸めアルゴリズムが適用されます。この動作は多少複雑に見えますが、対数の底に任意の数を使用可能にしながら、目盛りを読みやすく保つようにした結果です。

たとえば、上のプロットでは対数の底が 10 ですが、当然、底が２、x などの対数も考えられます。